Entropy and Information
Ujjwal Gyawali • 08 March, 2021
Entropy, much more than randomness.

Entropy is often times interpreted as the disorderness of a system. While this approach is intuitive and meaningful in the realm of physics and chemistry, it offers little to no help in the field computer science and communication. In this article we will try to look at entropy from a new a perspective of surprise and as a measure of quantification of this surprise introduced by Claude Shannon in his famous 1948 paper “Mathematical Theory of Communication” now known as The Information Theory. We will try to derive an intuitive understanding of this entropy. We will look at relevant examples and limit on use of the mathematical symbols and avoid formula whenever possible.
But firstly, we need to understand what information is and what a message is and what an event is. A message is anything that provides meaningful information and information is what helps us resolve uncertainty about an event. An event then is nothing but the occurrence of an instance out of many possibilities. An event can be a flip of a coin, a roll of a dice or anything of this sort. We communicate through messages to convey information about an event, to know with certainty the state of a system which was previously unknown to us. These are the abstract definitions of the terms upon which we will be working on.
So how do we know about the state of any system? By asking questions. What sort of questions? Throughout this article, we limit ourselves to Yes/No questions because it’s easier to map our possible responses to bits(1s and 0s) if we were communicating over large distances.
Now, back to Claude Shannon. His information theory builds upon this quantification of information carried in a message.
Before we receive any message, we have some guesses about the event. Our guesses could be completely random but often times we can anticipate the likelihood of certain events based on some initial knowledge about the system. We rely on the weather broadcast from the radio station to know what the weather will be like and to decide on whether or not to carry an umbrella to work. If we were living in a desert what amount of information about the weather would we expect from the radio station? None, right? Because it’s a desert, there is no uncertainty to be resolved. The message from the station adds nothing to what we already know irrespective of the length of the message.

It’s important that we emphasize on this length of message because it’s often times misinterpreted as entropy. While the terms entropy and message length use the same unit of measure(bits) and are associated, they are not the same thing. Entropy is what measures in bits, the average amount of useful information that can be derived from a set of events while the message can have any number of bits based on the coding strategy and has nothing to do with the actual information. Like with the example above, the radio station can use different coding strategies like: ‘SUNNY’ or ‘THE WEATHER WILL BE SUNNY’ or simply ‘1’ for sunny and still provide no meaningful information.
Now that we are all set up with this notion of information, we will now look at what it means to quantify this information, this idea of measuring how much surprise there is in an event.
Entropy as Yes/No questions
As we discussed earlier, all we care about is the meaningful information that helps us resolve uncertainty and know the state of the system. The system can be the weather or the result of a presidential election or anything. Suppose we live in a city that has the following likelihood for weather at any given day
Sunny: 50% , Rainy: 25%, Stormy: 12.5%, Cloudy(with no rain): 12.5%.
How many questions do we need to ask before we can know the weather with absolute certainty?… 4 ?? maybe 3. We can always be sure of the weather with these 3 questions
is it sunny?
is it rainy?
is it stormy?
But if we are really smart about it, we can work with 2 questions. How?
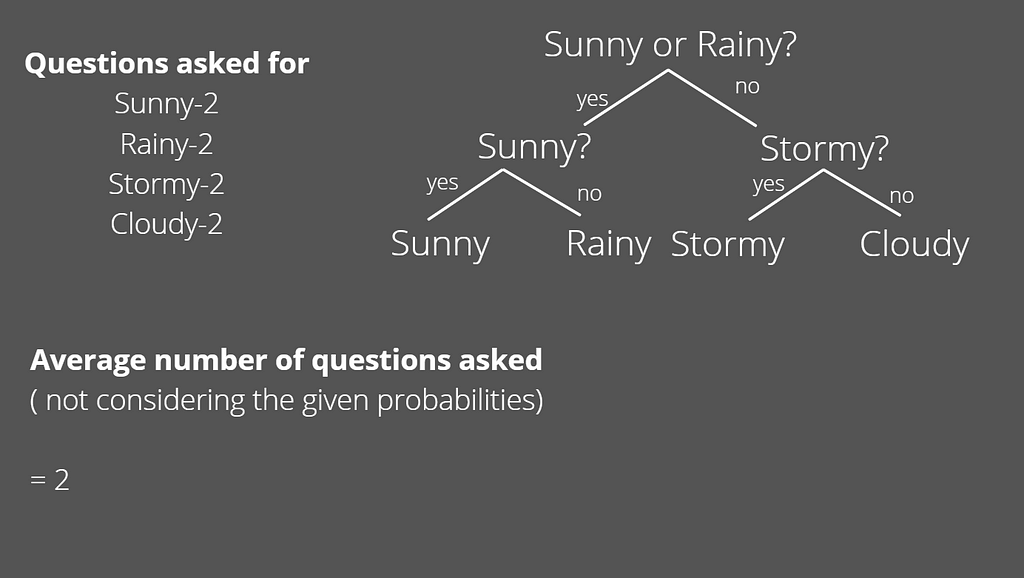
Even smarter if we take into account the likelihood for each weather.
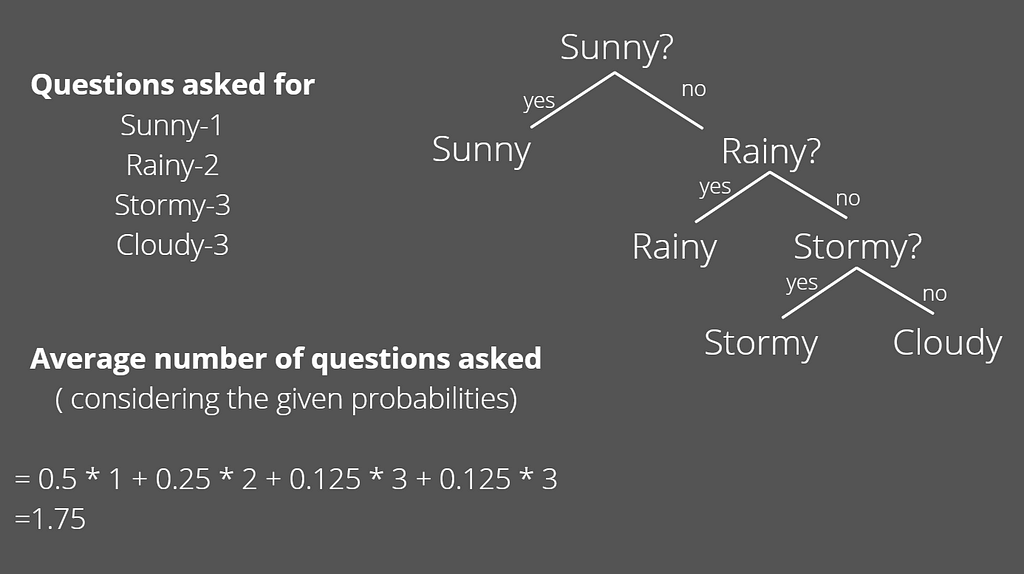
As we can see by taking into consideration the probabilities, we arrive at the optimal solution i.e. the least number of questions that can resolve our uncertainty about the weather. This minimum number of questions that is needed to know the state is the entropy for the system and is measured in bits.
Entropy as a function of probability
Taking the same example as above, we are 25% sure that it will rain. It is only upon receiving the broadcast message from the station “It will rain”, that we can be sure of the rain and our uncertainty is resolved by a factor of 4 i.e. 1/ 0.25. The information content in this message can be now calculated as
Information = log2(uncertainity_decrement_factor)
= log2(4)
= -log2(1/4)
= -log2(0.25)
= 2 bits
Notice how we have derived a measure of information for an event with probability, p. In general, information for an event x with probability p(x) is calculated as
H(x) = -log2(p(x))
Why do we use log? and why base 2?? We could have just used our uncertainty_decrement_factor as a measure for the information. But think of events that are super rare like the ones with probability of say 0.000000125. The uncertainty factor in this case would be 1/0.000000125 i.e. 8,000,000, a large number to work with. But simply plugging it to the log function gives us 22.93, much better, isn’t it?? and less straining in the eyes. But why base 2? Well there are many answers to it in the internet ranging from “we can use log with any base” to “it’s attributed to the use of bits as message symbols”.
According to Shannon, to transmit one bit of information is to reduce the recipient’s uncertainty by a factor of two. Like with our example above with the yes/no questions. So by log2(1/p(x)) what we are finding is how many bits(1s and 0s; message symbols) of information is required to resolve our uncertainty by a factor of 1/p(x). We are finding how many yes/no questions at the least do we need to answer to resolve the uncertainty by this factor. Also it allows us to use the same unit of measure as message length, that helps compare the goodness of message code by analyzing what portion of message carries the useful information and what portion is actually redundant.
We can see that information will be zero when the probability of an event is 1 i.e. there is no surprise. Refer to the example we discussed earlier the one with the desert. Also, we can see that learning that an unlikely event has occurred is more informative than learning that a likely event has occurred.
We made it !! But where is entropy? Entropy is simply the averages of the information for all the likely events. We now calculate the information for sunny, stormy and cloudy in similar fashion and find them to be 1 bit, 3 bits and 3 bits respectively. The average is then calculated as
Entropy = Summation ( p(x) * Information(x) )
= 1.75 bits
It’s the same entropy we calculated before by asking yes/no questions.
But how is entropy different from information? And why this average? While information is concerned with resolving the uncertainty of a single event at a time, entropy summarizes the uncertainty for all the possible events in a distribution. The intuition is that we are communicating a variable, entropy summarizes the information in the probability distribution for all events of a variable and not any single event that is communicated at a time.
Further readings:
A Gentle Introduction to Information Entropy (machinelearningmastery.com)
A Short Introduction to Entropy, Cross-Entropy and KL-Divergence — YouTube
Information entropy | Journey into information theory | Computer Science | Khan Academy — YouTube